扇形面积计算公式是什么

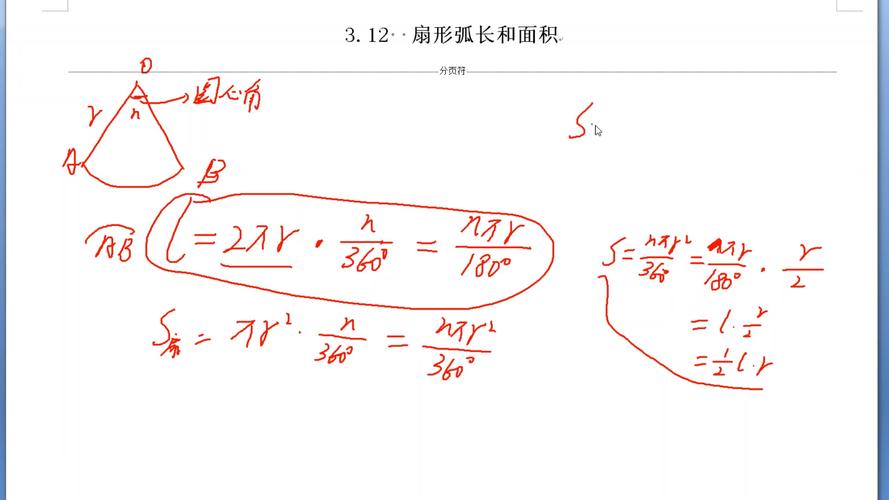
扇形的面积可以通过以下公式计算：S = (nπR²) / 360 或 S = (LR) / 2。其中，π代表圆周率，R代表扇形底圆的半径，n代表圆心角的度数，L代表弧长。对于n度的扇形，对应的弧长为：L = (n · 2πR) / 360。扇形是由圆周的一部分和对应的圆心角所包围的图形，也可以理解为由圆心角的两边和这两边所截的圆弧组成。这个定义也可以在《几何原本》中找到。