tanx的平方的原函数是什么

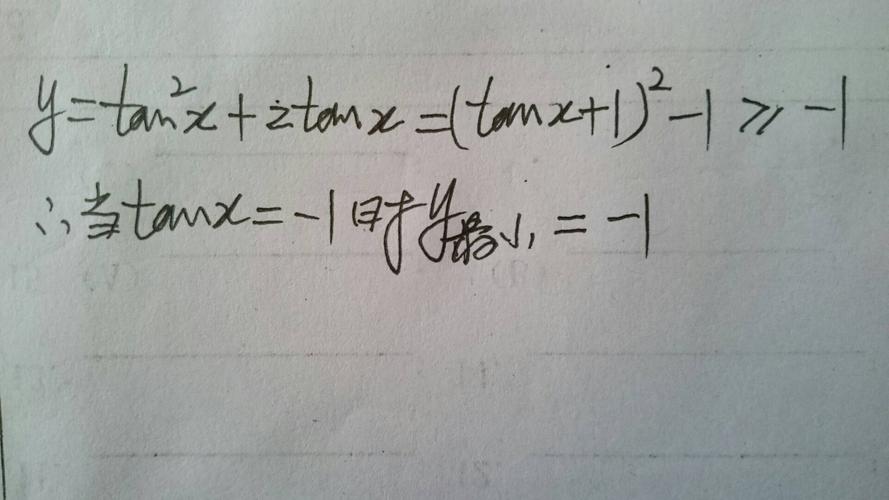
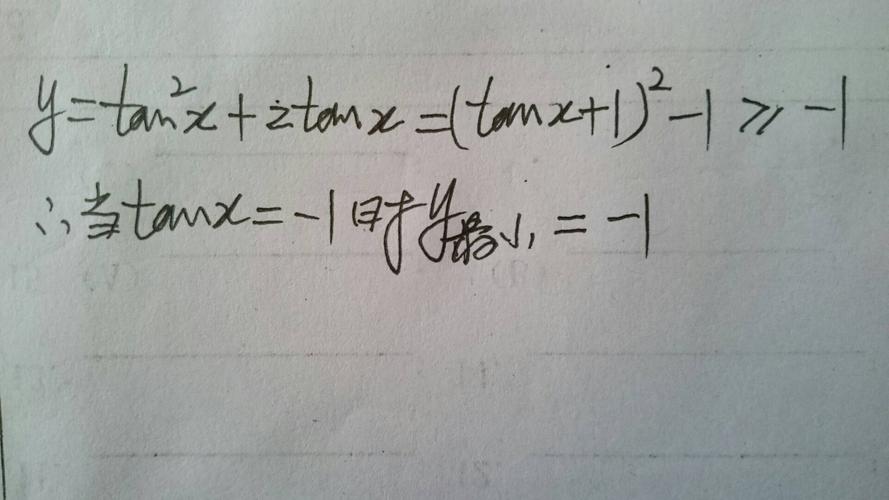
tanx-y C。原式是指对于一个定义在某区间的已知式子y，如果存在可导函数Y(x)，使得在该区间内的任一点都存在dY(x)=ydx，则在该区间内就称函数Y(x)为函数y的原式。 函数族Y(x) C(C为任一个常数）中的任一个函数一定是y的原式，故若函数y有原式，那么其原式为无穷多个。若函数y在某区间上连续，则y在该区间内必存在原式，这是一个充分而不必要条件，也称为“原式存在定理”。