微积分中的d是什么含义啊

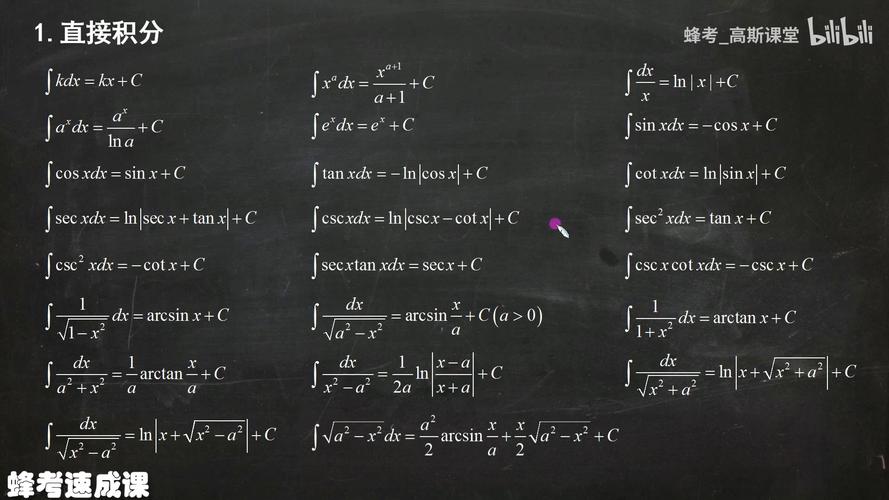
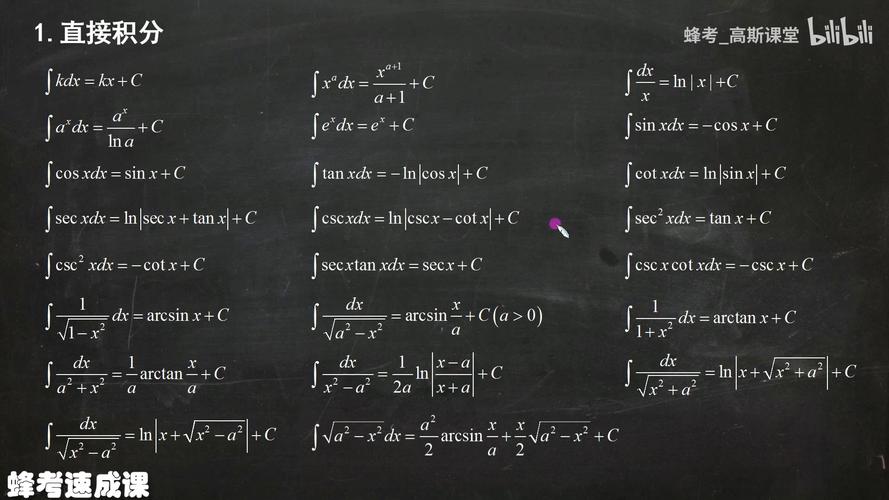
微积分中的微分来源于”差距”的英文单词”difference”。当这个差距趋向于无限小时，就发展成了”微分”，意味着无限小。微分是一个过程，是不断无限地进行分割和区分的过程。微分的概念是为了解决直线与曲线的矛盾而产生的，它在微小的局部区域可以使用直线来近似代替曲线，直接的应用就是将函数线性化。微分具有双重意义：一方面，它表示微小的量，使得我们可以将线性函数的数值结果作为原始函数的近似值；另一方面，它作为一种基本思想，用微分方法进行近似计算。