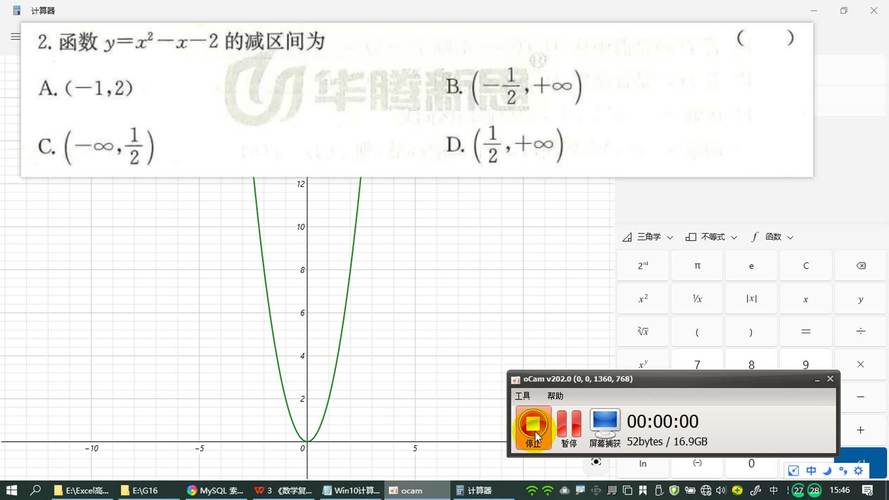
求解单调区间的方法有三种:
1、可以通过观察已知函数的函数图象来求解单调区间。常见的函数包括一次函数、二次函数、反比例函数、指数函数、对数函数、幂函数以及对勾函数。通过观察函数图象的形状和曲线的走势,可以确定函数的单调性和单调区间。
2、可以利用复合函数的单调性,根据同增异减的规律来求解单调区间。复合函数是由多个函数组成的函数,根据复合函数的性质,如果内层函数单调递增,外层函数也单调递增;如果内层函数单调递减,外层函数也单调递减。通过观察函数的构成和复合函数的性质,可以确定函数的单调性和单调区间。
3、可以利用导数来求解单调区间。首先确定函数的定义域,并计算函数的导数。当导数大于0时,函数为增函数;当导数小于0时,函数为减函数。通过导数的符号和函数的定义域,可以确定函数的单调性和单调区间。