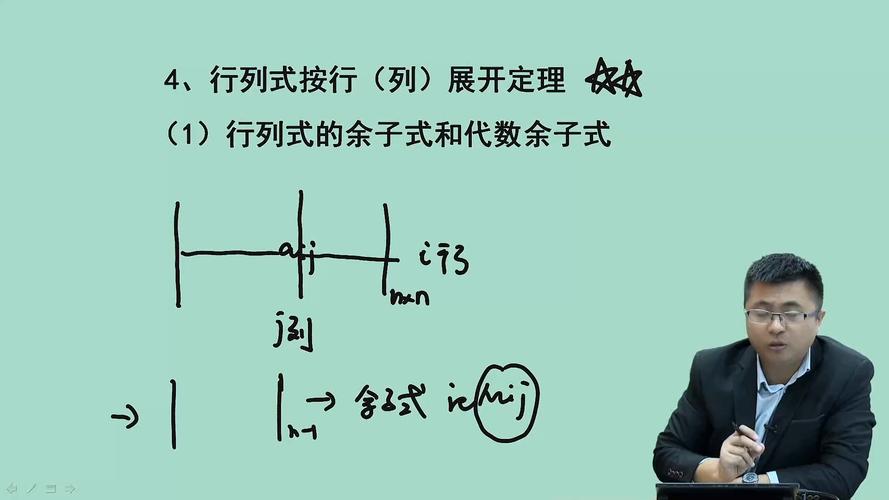
一个矩阵A的余子式,指的是在矩阵中划掉某一行和某一列后,剩下的部分的行列式。特别地,对于一个n阶矩阵A,其第i行第j列的余子式,记作M(i, j),是将第i行和第j列划掉后所得到的(n-1)阶矩阵的行列式。
更具体地说,给定一个m×n的矩阵A,其中m≤n,如果m=n,那么A的k阶余子式指的是去掉了A中一个大小为k的子矩阵所在的行和列后所得到的(n-k)×(n-k)矩阵的行列式。这个k阶子矩阵可以是在任意位置,但是所在行和列的数量分别为k。
对于给定的n阶矩阵A,我们可以用代数余子式的概念来求解行列式。特别地,第n行的代数余子式之和等于将A的第n行的元素都换为1所得到的行列式。这意味着我们可以通过逐个将第n行的元素替换为1来计算所有代数余子式,并将它们相加,得到行列式的解。
以上是关于矩阵的余子式和求解方法的相关内容。